【Sieve of Eratosthenes】Fast Factorization & CountNonDivisible & CountSemiprimes

2014-07-05

##Sieve of Eratosthenes Sieve of Eratosthenes是用于寻找n以内所有素数的一种简单有效方法。 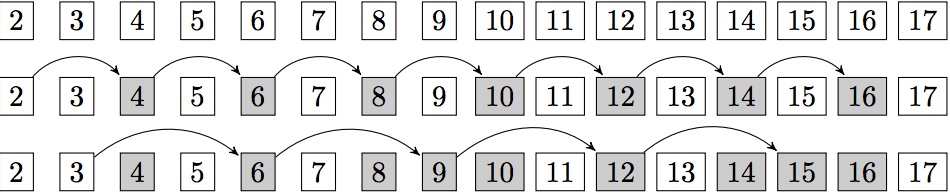在筛3的倍数时6肯定已经被筛掉了，因此可以从3*3开始筛 算法复杂度是O(n log log n)，证明比较复杂。

1 def sieve(n):
2 	sieve = [True] * (n + 1)
3 	sieve[0] = sieve[1] = False
4 	i = 2
5 	while (i * i <= n):
6 		if (sieve[i]):
7 			k = i * i
8 			while (k <= n):
9 				sieve[k] = False
10 				k += i
11 		i += 1
12 	return sieve

##Fast Factorization Factorization是指将给定数分解为素数因子之积

1. 可以修改Sieve算法，每次消去一个数的时候，我们记录下它的最小prime因子。
2. 假如数x的最小素数因子是p，那么我们再寻找x/p的最小素数因子，递归。一个数的prime factor大于2，因此其因子总数不会超过log x，因此这一步是 O(log x)

1 def arrayF(n):
2 	F = [0] * (n + 1)
3 	i = 2
4 	while (i * i <= n):
5 		if (F[i] == 0):
6 			k = i * i
7 			while (k <= n):
8 				if (F[k] == 0):
9 					F[k] = i;
10 				k += i
11 		i += 1
12 	return F

1 def factorization(x, F):
2 	primeFactors = []
3 	while (F[x] > 0):
4 		primeFactors += [F[x]]
5 		x /= F[x]
6 	primeFactors += [x]
7 	return primeFactors

##CountNonDivisible

You are given a non-empty zero-indexed array A consisting of N integers.

For each number A[i] such that 0 ≤ i < N, we want to count the number of elements of the array that are not the divisors of A[i]. We say that these elements are non-divisors.

For example, consider integer N = 5 and array A such that:

 A[0] = 3 A[1] = 1 A[2] = 2 A[3] = 3 A[4] = 6

For the following elements:

• A[0] = 3, the non-divisors are: 2, 6,
• A[1] = 1, the non-divisors are: 3, 2, 3, 6,
• A[2] = 2, the non-divisors are: 3, 3, 6,
• A[3] = 3, the non-divisors are: 2, 6,
• A[6] = 6, there aren't any non-divisors.

Assume that the following declarations are given:

struct Results {
  int * C;
  int L;
};

Write a function:

struct Results solution(int A[], int N);

that, given a non-empty zero-indexed array A consisting of N integers, returns a sequence of integers representing the amount of non-divisors.

The sequence should be returned as:

• a structure Results (in C), or
• a vector of integers (in C++), or
• a record Results (in Pascal), or
• an array of integers (in any other programming language).

For example, given:

 A[0] = 3 A[1] = 1 A[2] = 2 A[3] = 3 A[4] = 6

the function should return [2, 4, 3, 2, 0], as explained above.

Assume that:

• N is an integer within the range [1..50,000];
• each element of array A is an integer within the range [1..2 * N].

Complexity:

• expected worst-case time complexity is O(N*log(N));
• expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).

Elements of input arrays can be modified.

</br>

###思路 初步想法是，把数组排序，然后用Sieve方法求出其divisors，并同时记录并更新数组中元素的divisors个数，stackoverflow上的讨论看上去极其复杂, CountSemiprimes的解法倒是比较有意思